In this article, we will clarify some misconceptions about stress, density, and other influencing factors.
The speed of sound is the distance traveled by sound waves per second in a flexible medium. These media are made up of many molecules and are tightly bound together by the attraction between the molecules. Sound propagates through the compression and expansion of these molecular structures.
Pressure and density effects
The speed at which sound waves travel through the medium is primarily affected by the stiffness and density of the medium.
Hardness is the resistance when describing a substance under uniform pressure. The unit is Pascal, and 1 Pa is equal to 1 Newtons per square meter (about 0.1 kg per square meter or 0.02 pounds per square foot). Density is the ratio of material weight to volume in kg/m3.
In general, the speed at which sound waves travel in a medium (solid, liquid or gas) can be calculated by Equation 1:

Where c is the speed of sound, the unit is m/s; K is the uncompressible rate, the unit is Pascal; Ï is the density, the unit is kg/m3
From the equation we can see that the speed of sound becomes faster as the incompressibility (stiffness) increases, and becomes slower as the density increases.
We all know that sound travels faster in water than in air. The density of water at room temperature is 800 times that of air. Calculating the seemingly higher density according to Equation 1 should slow the speed of sound, but the opposite is true. This is because with a relatively small increase in density, the stiffness of water is much greater than air (more than 1500 times), so the speed of sound travels in water is about four times faster than in air.
From Equation 1, we know that the media density is closely related to the speed of sound. Since the air pressure and air density vary with altitude, a common misconception arises – we need to set different delays on Mount Everest and the Riviera.
The air behaves the same as the ideal gas when it propagates sound waves. The relationship between the pressure and the density of an ideal gas is as shown in Equation 2, and this equation is established as long as the thermodynamic properties of the medium do not change (the molecular arrangement and volume of the medium do not change).
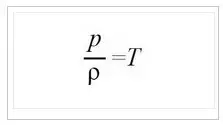
Where p is the pressure in Pascal; Ï is the density in kg/m3; T is the temperature in Kelvin
The Kelvin temperature scale can be converted to the Celsius temperature scale by conversion, and the lowest scale of the Kelvin temperature scale is 0 degrees = -273.15 degrees Celsius (-459.67 degrees Fahrenheit). There is a negative correlation between the pressure and density of the gas propagation medium. The pressure and density in Equation 2 are proportional in the case where the temperature remains constant. The pressure and density ratios in the equation are defined by temperature and remain synchronous.
The stiffness coefficient of air mentioned in Equation 1 is proportional to the pressure. As the pressure increases, the elasticity of the medium decreases (hardness increases) and the speed of sound increases. However, as the pressure increases, the density of the medium also changes and the speed of sound slows down, thereby forming a phenomenon in which the actual speed of sound does not change (the air temperature remains unchanged). Therefore, the speed of sound propagation in Johannesburg at an altitude of 1750m and in Amsterdam at sea level is virtually the same (under the same temperature conditions).
Temperature effect
Let us look at the effect of temperature on the speed of sound while maintaining a constant volume and volume (density remains constant).
An increase in temperature accelerates the movement of air molecules and increases the pressure, thereby reducing the coefficient of elasticity of the air and increasing the speed of sound. Equation 3 is capable of accurately calculating the speed of sound when the temperature of the relatively dry air changes, and the factors of the thermodynamic properties of the medium have been taken into account.
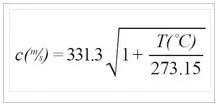
Where c is the speed of sound in m/s; T is the temperature in degrees Celsius
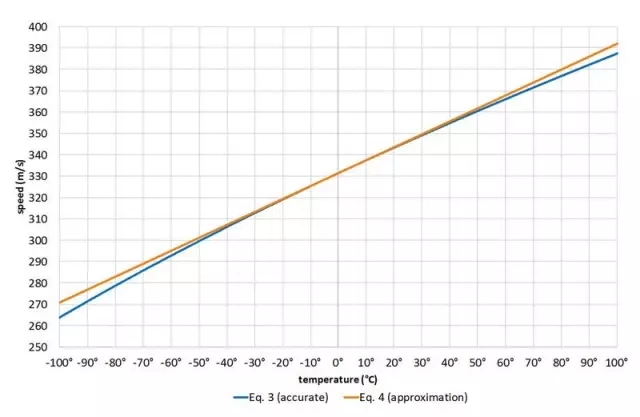
In general, you can use a simplified formula to calculate the speed of sound (Equation 4):

Where c is the speed of sound in m/s; T is the temperature in degrees Celsius
In the field sound application, the calculation result of the simplified formula with 0.5% accuracy can already meet the usage requirements. It can be seen from the following figure that the calculation result is very close to Equation 3.
Humidity effect
In the previous section we explored the interaction between pressure and density under the premise that temperature and structural/thermodynamic properties remain constant.
Let us now look at the effect of humidity on the structure/thermodynamic properties of the media. Before we used the different conditions of the mountains and the sea to explain, we now use the desert and the rainforest for comparison.
Typical media include air (a mixture of oxygen, nitrogen, and other components) and water. The term humidity describes the ratio of water vapor to air. The proportion of water vapor contained in the "high" air is greater than the "low" air humidity. Therefore, the change in humidity actually changes the composition of the media.
The mixture of water vapor and air has a lower elasticity (higher stiffness) than air, which increases the speed of sound. Since the molar mass of water vapor (atomic density) is less than that of dry air, the density of moist air is lower than that of dry air, which also increases the speed of sound.
However, the thermodynamic properties of water have some subtle differences from oxygen and nitrogen. Therefore, the change in humidity is not only a change in pressure and density, but also a change in the transmission characteristics of the medium, and this change in transmission characteristics also causes the speed of sound to slow down.
In summary, we can say that the increase in humidity will increase the speed of sound slightly. That is to say, the sound travels in humid air faster than in dry air. However, the speed of sound changes very little and does not actually affect the performance of the sound reinforcement system.
Figure 2 graphically shows the effect of temperature and relative humidity on the speed of sound. The chart uses color partitioning to represent a change in sound velocity (approximately 0.3%) with an accuracy of 1 m/sec, from the driest desert (0%) to the area where the moisture in the air reaches saturation and forms a cloud (100%).
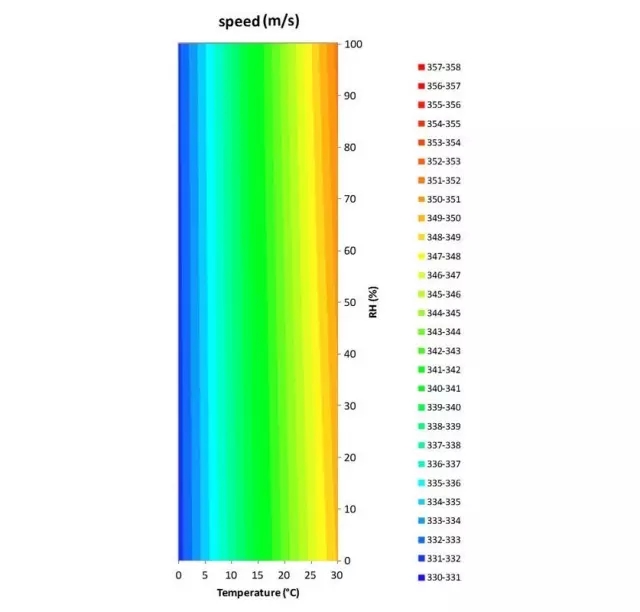
Figure 2: Sound velocity in wet air
From the left part of the chart (blue area, indicating cold, slow air conditions), you can see that even from the driest ice to the wettest ice (bottom to top), the speed of sound does not even occur. 1m/sec change. This is because in the case of saturation, the moisture content in the cold air is lower than that of hot air. The right side of the chart (red area, indicating rapid hot air conditions) shows that the transition from the Sahara to the Amazon rainforest has a large impact on the speed of sound, but the magnitude of this change is still minimal for sound reinforcement systems.
When the temperature is constant, the change in relative humidity reaches 100%, which causes the sound velocity to change by 1 m/sec. In fact, the increase in the number of umbrellas has a much greater impact on the quality of sound transmission than on sound speed.
From another perspective, the effect of the most severe humidity changes on sound velocity is about the same as a mild temperature change (about 1.7 degrees Celsius). Obviously, we don't need an altimeter and hygrometer to help us determine the delay parameters or estimate the sound velocity at the scene.
For all imaginable extreme weather conditions, we can use a thermometer and a calculator to estimate the speed of sound. The following two formulas have an error of less than 0.3%, or 1 meter (3 feet) per second.
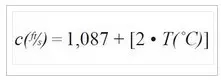
Where c is the speed of sound in feet per second; T is the temperature in degrees Celsius
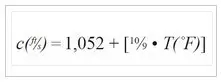
Where c is the speed of sound in feet per second; T is the temperature in degrees Fahrenheit
Online UPS provides continuous power to critical equipment, eliminating downtime during power outages. It offers protection against voltage fluctuations, spikes, and surges, making it ideal for data centers, hospitals, and other sensitive applications.
It is designed to protect sensitive electronics and prevent data loss or damage caused by sudden power disruptions.The primary function of an inverter UPS is to convert DC (Direct Current) power from a battery into AC (Alternating Current) power that can be used by electronic devices. This conversion is achieved through the use of an inverter, which changes the battery's DC power into the AC power required by the connected equipment.
Our Bosin Inverter with UPS function power frequency energy-saving transformer with full-bridge pure sine wave output, low loss and high efficiency.They can unattended duty-free function may also offer the ability to remotely manage and control the UPS, allowing users to monitor its status, perform diagnostics, and configure settings from a central location.Support a variety of communication interface, remote monitoring via RS232/mobile App/Wi-Fi/GPRS.Automatic start when city power comes.It has three working model:Grid prior, Eco mode, PV prior.
One of the key features of an inverter UPS is its ability to provide uninterrupted power during a blackout. When the main power supply is interrupted, the UPS automatically switches to battery power, ensuring that connected devices continue to operate without any interruption. This seamless transition is crucial for systems that cannot afford any downtime, such as servers, medical equipment, or communication networks.
backup power supply,Online Uninterruptible Power Supply, Industrial power protection, voltage regulation, battery backup
Bosin Power Limited , https://www.bosinsolar.com